“We learn more by looking for the answer to a question and not finding it than we do from learning the answer itself.”
Lloyd Alexander
An inquirer is someone who inquires, or in other words, they ask for information. Being an inquirer is one of the ten IB learner profile. As an inquirer, we learn beyond the classroom. When we are curious, we do independent research to foster and nurture our curiosity, and to obtain more knowledge.
Sequences and Series
When sitting in Maths class, studying about sequences and series, you may wonder why we need to study it and how it is useful for our day to day life. However, these sequences and series are actually everywhere and can be found in our daily lives.
Sequences and series. What’s the difference? Sequences is an ordered list of terms that are related to each other in some way. While series is the sum of terms in a sequence. There are plenty of different types of sequences and series, two of them being arithmetic and geometric.
What is the difference between arithmetic and geometric sequence?
| Arithmetic | Geometric |
| has a common difference between terms | has a common ratio between terms |
| addition or subtraction | multiplication or division |
| can only be divergent | can either be divergent or convergent |
What are divergent and convergent series? To differentiate them, we can correlate them to divergent and convergent thinking.
Convergent thinking is more linear and systematic. It narrows down multiple ideas into one single idea or solution. Divergent thinking is more creative and focuses more on the connection between ideas. It produces multiple answers and ideas to a single question.
Relating to that, when a series is convergent, the sequence of its partial sums approaches a real number, in other words, it approaches a limit. If a series doesn’t converge, it is a divergent series. A divergent series doesn’t have a limit that is finite, meaning that it is infinite.
Sum of Infinite Geometric Series
Is it possible to find the sum of an infinite geometric series?
Keeping in mind that the formula to find a tern in a geometric sequence is Un = U1 rn-1 . It is only possible if the common ratio is more than -1 but less than 1, and it cannot be 0 ( -1 < r < 1 , r ≠ 0). Why is it not possible to for the ratio to be 0? Here is why:
U2 = U1(0)2-1 = U1 (0)1 = 0
U3 = U1(0)3-1 = U1 (0)2 = 0
U4 = U1(0)4-1 = U1 (0)3 = 0
To find the ratio:
r = 0/0 = 0/0
But, 0/0 is “indeterminate”, which is why it is not possible for the common ratio to be 0. Hence, it can be written as | r | < 1 . This formula can be used to find the sum of an infinite geometric series:
As stated in the table above, it is possible for a geometric series to be divergent, and a divergent series isn’t converging. Which is why it is possible to find the sum of an infinite geometric series.
Real-life Applications of Sequences and Series
2048 game
In the game 2048, it involves combining tiles of the same number to get a bigger number. However, all these numbers are powers of 2, showing that it is a geometric sequence.

Taxi fare
When you get into a taxi, the taxi fare starts at a specific amount. But there is a fare, for example $0.50/km, and the total fare increases as you travel further and spend more time in the taxi (for example, when there is traffic). At the end of the ride, you the taxi meter will show you the total taxi fare, which is the sum of the flag down rate and distance rate. This is an example of arithmetic series.
As you can see, there is a lot of uses of sequences and series. Taxi fare and the 2048 games are just amongst two of the many applications of sequences and series. We can see that it is being used in our daily lives, from the games we play on our mobile phones, to transport, and even population growth, bank investments and interest rates, and carbon dating in the laboratory.
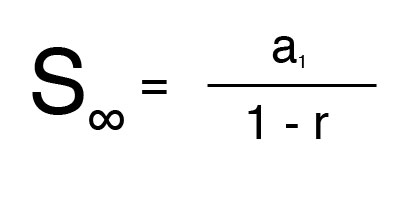
I found this blog particularly informative as you gave a number of examples to each problem being discussed. Other than that, you successfully classified the difference between arithmetic and geometric sequence. It is appealing that you used real-life examples, like the game 2048 as well as taxi fares. Additionally, you have summed up the sequences and series topic perfectly. This blog was really simple to understand yet it is written in a profoundly superb.
LikeLike
Truly a well explained blog about sequences and numbers! I like how you referred the game 2048 as a real life application of how sequences and numbers can be used. Im looking forward to more of your intruiging blogs!
LikeLike
Having have learnt about arithmetic sequences before, I had previously thought that that was all theres was to it. However, after reading this blog, I realized that arithmetic was a much vaster field and there were many concepts I had yet to learn. One of the things that was new to me was that arithmetic sequences were convergent. At that, the explanation provided for convergence and divergence was made really simple and clear for readers to digest. Geometric sequences was something I hadn’t explored into deep depth, so seeing as to that it had sticked in my mind that it was about common ratios using multiplication and division, that shows that you had done a great job in making the topics memorable to readers. Moreover, I thought that how you thoroughly wrote about 0 being impossible to be the common ratio of geometric sequences was very easily understandable, and even then the fact that you managed to keep me reading on is truly an achievement. Also, the real-life applications you gave were examples that were really common things which we could easily find in our daily lives so that anyone could effortlessly relate to it and see how sequences could be widely useful. A small suggestion I would give is to provide examples of arithmetic and geometric sequences in order to allow readers to further grasp the concept with tremendous ease. I had a great time combining concepts I have learnt in the past with new ones in this blog!
LikeLike