E-journal 3: Bicycle

Introduction

What is a function?

• Function is the relationship between two different sets of elements/variables (for example: x and y)

Types of Relation

(domain – input, range – output)

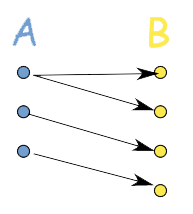
• One-to-one: when one domain corresponds to one range

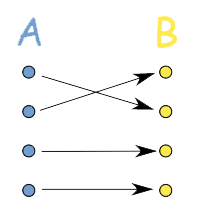
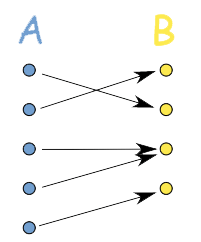
• One-to-many: when one domain corresponds to more than one range

• Many-to-one: when more than one domain corresponds to one range

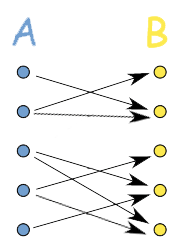
• Many-to-many: when more than one domain corresponds to more than one range

Relation or Function?

How do you know if a graph is a function or a relation? And are all relations a function?

To determine whether a graph is a function or not, we can do a test called the “vertical line test”.

The “vertical line test” is when you draw a vertical line at any point of the graph. If the vertical line only passes through one point on the graph, then the graph is a function. But if the vertical line passes through more than one point, then the graph is not considered a function. In other words, one value of of x (domain) can only have one value of y (range). Which means that only the relation “one-to-one” and “many-to-one” can be considered to be a function.

Types of Transformation in Functions

TRANSLATION

Vertical: y = f(x) + c

• If c>0, then the graph will move up by c units.
• If c<0, then the graph will move down by c units.

Horizontal: y = f(x+c)

• If c>0, then the graph will move to the left by c units.
• If c<0, then the graph will move to the right by c units.

REFLECTION

• y = -f(x), the graph will be reflected across the x-axis.
• y = f(-x), the graph will be reflected across the y-axis.

STRETCHING & COMPRESSING

Vertical: y = cf(x)

• If c>1, the graph will be stretched vertically by a factor of c.
• If 0<c<1, the graph will be compressed vertically by a factor of c.

Horizontal: y = f(cx)

• If c>1, the graph will be compressed horizontally by a factor of 1/c.
• If 0<c<1, the graph will be stretched horizontally by a factor of 1/c.

Graphing a Bicycle

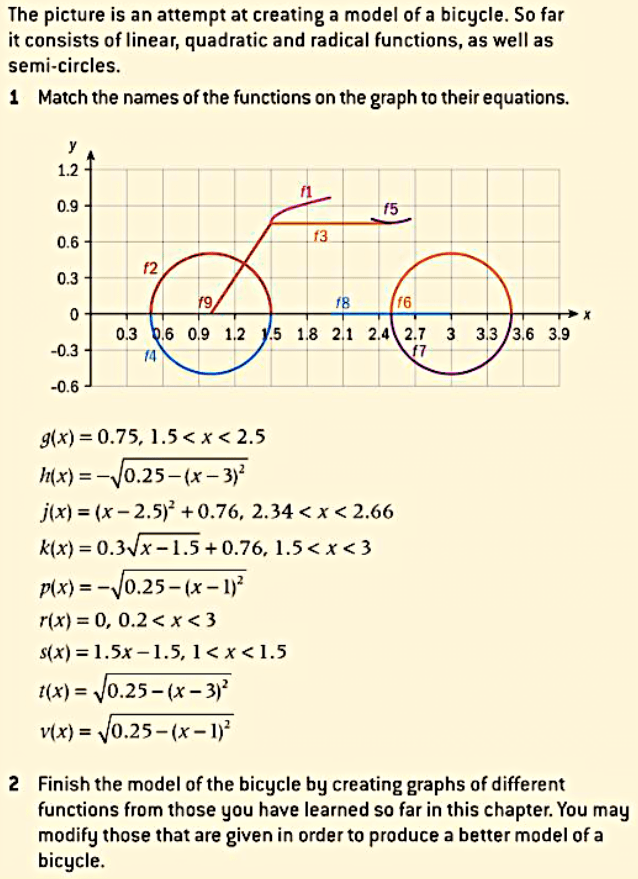
MATCHING THE GRAPHS TO THEIR RESPECTIVE EQUATIONS

• g(x) = f3
• h(x) = f7
• j(x) = f5
• k(x) = f1
• p(x) = f4
• r(x) = f8
• s(x) = f9
• t(x) = f6
• v(x) = f2

Using desmos, I graphed the equations above.

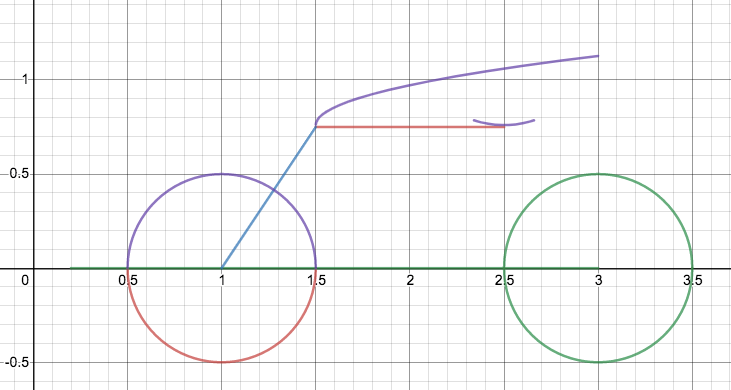
Not being satisfied with how the bicycle looks, I added more functions and changed some of the functions.

These are all the functions I added:

And I also changed up 3 functions to make the bicycle look better.

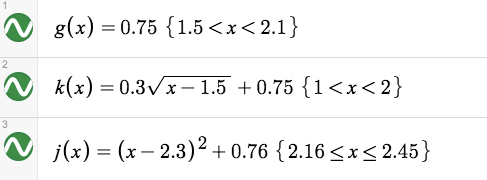
Finally, the bicycle looked like this:

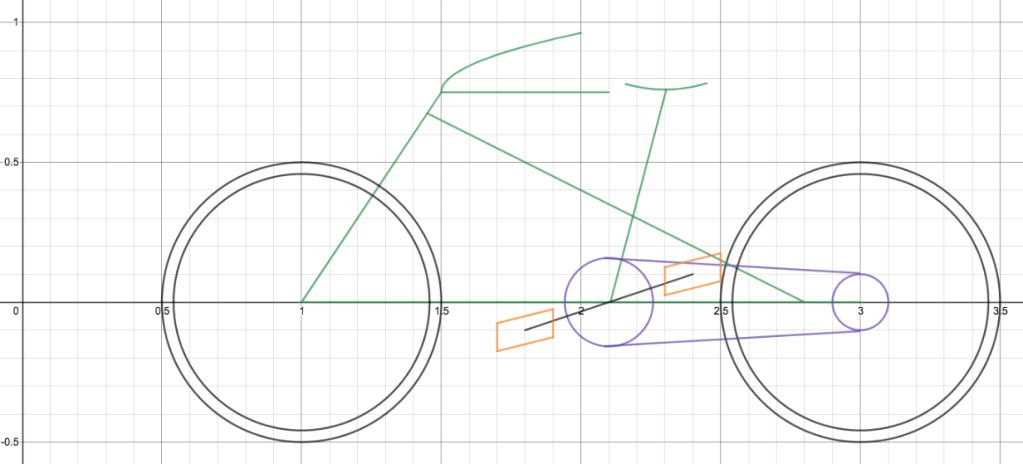
REAL-LIFE APPLICATIONS

VENDING MACHINE

• The input will be the the money and the output will be the object we bought from the vending machine

EARNING MONEY

• The input is the amount of time you put into work to earn money and the output is the amount of money (salary) you will get from those hours you worked.

CONVERSION

• For example, the conversion of temperature from Celsius to Fahrenheit.
• The formula is F = 1.8C + 32, where F is the temperature in Fahrenheit and C is the temperature in Celsius.
• Let’s say we want to convert 100°C to Fahrenheit, we input the value C=100.
• F = 1.8(100) + 32 = 212
• Thus, 100°C is equivalent to 212°F.
• This is an example of function since the input would be the temperature in Celsius and the output is the temperature in Fahrenheit.

IB Learner Profiles

INQUIRERS

Being curious and playing around with functions to figure out how to make a bicycle only from the functions we have learned like quadratic function. And also playing around with their limits and restrictions.

THINKERS

Critically thinking on how to transform functions and form equations to make a bicycle.

COMMUNICATORS

Conveying the knowledge we have learned in Maths class to a blog and teaching others about it.

RISK TAKER

Submitting the blog a couple minutes before the deadline 🙂

References:

• https://www.mathsisfun.com/sets/function-transformations.html
• https://sis-kg.kognity.com/study/app/ibdp-mathematics-analysis-and-approaches-hl/functions/functions/the-concept-of-a-function/
• https://www.mathsisfun.com/sets/injective-surjective-bijective.html