E-journal 6: Fundamental Theorem of Calculus

Introduction

Back when I took IGCSE Additional Mathematics in Sec 3 and 4, seeing that I had to learn calculus and the idea of it freaked me out. Everybody has always said how challenging it was. When I first started learning it, yes, it was hard, but eventually, it became one of my favorite Maths topic to study. Solving calculus problems is like solving a puzzle, which I really enjoy.

My seniors have always told me how insanely difficult IB Maths HL calculus was. So when we started diving into calculus this semester, I was intimidated, even though I had understood calculus in Add. Maths and understood it well (plus add the fact that we had to learn calculus in an online school setting). However, at the same time, I won’t deny that I felt pretty excited to revisit calculus once again. Calculus was actually a big part of why I decided to take MAAHL instead of MAIHL (calculus is wayyyy better than statistics :D).

Toolkit Presentation

In MAAHL, we have to do something called as toolkit, which is essentially a set of questions that we not only have to answer, but also have to investigate and research upon. Toolkits can go one of the two ways for me: it can stress me out or I can find it interesting. Well in this case, it was a relatively more fun toolkit compared to the ones we have done previously.

In this toolkit, the class was divided into 3 groups. My group had to discuss and present regarding the Riemann Sum. Our presentation is attached below.

A quick summary of Riemann’s sum

Riemann’s sum can be used to find the area under the curve by using rectangles. As the number of rectangles increases, the area will become more accurate. However, it’s important to note that no matter how many rectangles are used, it’s only an approximation, so the area will only approach the exact value but will never be equal.

Fundamental Theorem of Calculus

The Fundamental Theorem of Calculus is essentially the relationship between differentiation and integration, which was discovered by Sir Isaac Newton and Gottfried Wilhelm Leibniz.

The First Fundamental Theorem of Calculus

This theorem states that if f is continuous on the closed interval [a, b] and F is the indefinite integral of f on [a, b], then

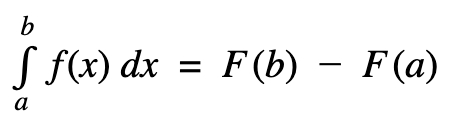
This means that if function f (the integrand) is continuous between the points a and b (including points a and b), then the value will be equal to the indefinite integral at the closed interval [a, b] when integrated.

The Second Fundamental Theorem of Calculus

This theorem states that if f is continuous on an open interval and point a is a point at the open interval, then F is defined as

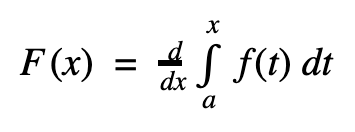
then

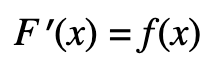
at point a.

These two shows the relationship between differentiation and integration, and the connection between definite and indefinite integrals’s analytic and geometric components. It also allows us to perform certain “tasks” easier, for example, finding the area under the curve. Not only will it give an exact value of the area but it’s also way less tedious and much easier compared to the Riemann’s sum.

International Mindedness

• 

• 

• 

• 

• 

• 

As mentioned above, the discovery and development of calculus is credited to two people – Sir Isaac Newton and Gottfried Wilhelm Leibniz in the 17th century. It’s believed that they investigated calculus independently, and that Leibniz only discovered calculus 8 years after Newton did. However, let’s go back in time.

During the ancient period, more specifically between 580-212 BCE, algebra and geometry were created by 3 philosophers – Archimedes, Euclid, and Pythagoras. You’ve probably heard their names before as they’re often associated with the Pythagoras’ Theorem and Euclidean geometry. However, at this point, the basic operations of maths and the numbering system has not been invented yet. So they struggled in unifying algebra and geometry, that was until Rene Descartes (late 1500s). He not only unified algebra, but also found other groundbreaking concepts such as that two numbers can be used to describe the coordinates on a 2D plane.

Moving back to the 17th century, to the calculus discovery era. How was it discovered? Well, Newton calculus followed his work of the laws of motion and gravitation. His conceptual understanding in physics allowed him to create relationships between mathematics and physical phenomena, leading him to discover the world of calculus.

Real-Life Applications

Calculus is pretty versatile as it can be applied in a wide range of scenarios and in different areas, such as biology, chemistry, physics, business, and even music.

• Tumor growth – Since calculus allows us to calculate the rates of change, it allows oncologists and physicians to calculate the rate of tumor growth or shrinkage, and also how many cells are in the tumor, which can help doctors determine the best course of treatment for cancer patients, analyze how rapidly the cancer is progressing, and more.
• Epidemiology – Taking in the example of the coronavirus, scientists are able to calculate how fast the virus is spreading, how far it can spread, how to contain it, and more, by using calculus.
• Space exploration – Before going on a space mission, scientists calculate various factors such as different orbiting velocities, and distant of target planet, using calculus to figure out the sun and moon’s gravitational influence.
• Astronomy – Calculus can be used to study the motions of various space objects such as planets and meteors, and the rate at which it is moving.
• Harmonics – In music, damped harmonic motion an be calculated through calculus. Friction and air resistance can cause oscillation energy to dissipate, and this dissipative forces is known as damped force. This damped force is proportional to an object’s velocity.
• Prosecution case planning – Even lawyers can utilize calculus to build disciplines, which is used to solve prosecution cases.

IB Learner Profiles

• Communicators – I learned to express myself and communicate with others through many aspects, such as writing this blog, during the presentation of the toolkit, and even during discussions with my toolkit group.
• Knowledgeable – Other than having conceptual understanding and knowledge, I also explored other aspects such as the brief history of calculus, and even how calculus can be used in many different subject areas.
• Inquirers – Throughout this blog, I learned to research and to answer my own inquiries that popped up by researching, essentially nurturing my curiosity. Additionally, I not only learned to study independently, but also learned to study as a group when doing the toolkit.
• Thinkers – The nature of the toolkit and any e-journal is that it’s not just a straight forward answer and usually requires a lot of research. Thus, I learned to solve complex problems and analyze them through creative, analytical and critical thinking skills.
• Reflective – After finishing the toolkit, I was able to reflect back and identify my own personal strengths and weaknesses.
• Open-minded – As with group work, there are many different people with different ideas. When discussing, I’m willing to listen to what my group mates have to say because it might be a better idea than mine and I can always learn something new from them.

Sources

• https://math.libretexts.org/Bookshelves/Calculus/Book%3A_Calculus_(OpenStax)/05%3A_Integration/5.3%3A_The_Fundamental_Theorem_of_Calculus
• https://mathworld.wolfram.com/FundamentalTheoremsofCalculus.html
• https://futurism.com/how-and-why-did-newton-develop-such-a-complicated-math
• https://allusesof.com/math/51-amazing-uses-of-calculus-in-real-life/