During our iGCSE years, our Maths teacher have probably drawn this diagram when we were studying numbers.
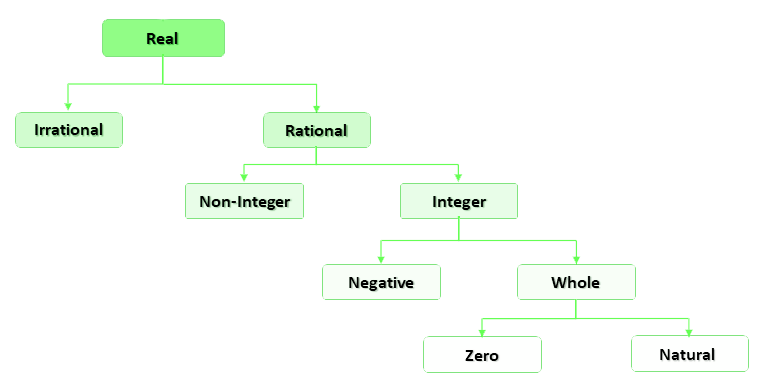
We have learned that irrational numbers are numbers like π. But, there is actually more to it. Beyond real numbers, there are imaginary numbers. This is what the diagram would look like.
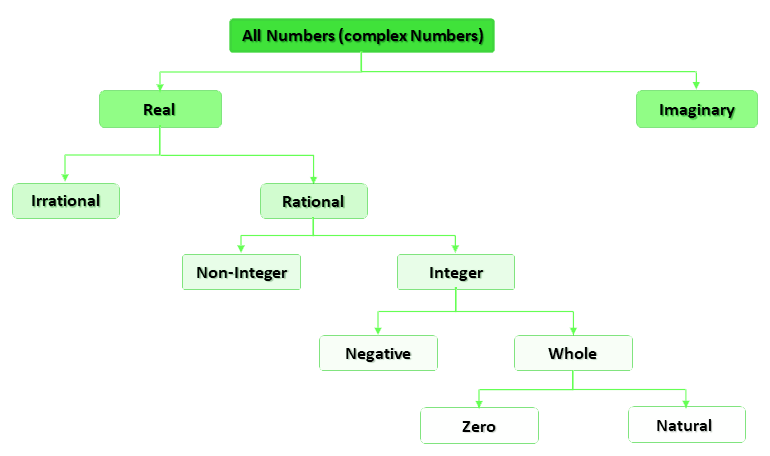
Both real numbers and imaginary numbers make up complex numbers. But before we get to complex numbers, what are imaginary numbers?
Imaginary Numbers
Imaginary numbers is the square of a negative number, meaning that if you square imaginary numbers, you will get a negative number. Whenever you root a negative number in your scientific calculator, the screen will say “math error”. However, if you press MODE, then 2 (CMPLX), it is going to change your calculator set up to “CMPLX” mode. Once you do this and root a negative number, you will get an answer in terms of i, making it possible to root a negative number.

Example: (calculator in “CMPLX” mode)
√(-5) = √5i
You may also have seen i whenever you solve quadratic equations using your calculator (MODE -> 5 (EQN) -> 3, then input the values of a, b ,and c). If your quadratic equations have negative roots or no solutions, you will see i in your calculator.
Example:
x^2 + 4x + 5 = 0
x = -2+i OR x = -2-i
What if you don’t use calculator, but use the quadratic formula instead? You can still use i. Here is an example.
Complex Numbers
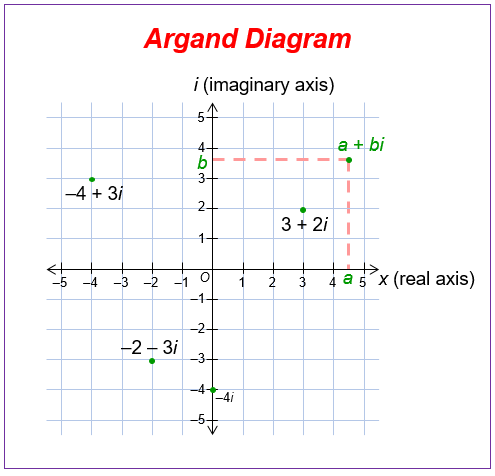
Now that we know what imaginary numbers are, what are complex numbers? Complex numbers are numbers that have a real number and an imaginary number. It can be written in the form of a+bi, where a is the real number, and b is the imaginary number. This is known as the Cartesian form.
Example:
z = 5 + 7i
Real part of z = Re(z) = 5
Imaginary part of z = Im(z) = 7
Using the Cartesian form, we can plot complex numbers into a complex plane or Argand diagram. This is similar to the Cartesian plane we all know about, but the Argand diagram is for complex numbers, where the x-axis is for the real part, and the y-axis is for the imaginary part.
Modulus-argument Form
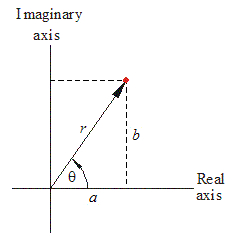
Other than the cartesian form, z or complex number can be written in modulus-argument form, also known as polar form.
Modulus-argument form:
z = rcis θ = r (cosθ + isinθ) , where r is the modulus of z or |z| and θ is the argument of z or arg(z).
r = √(a^2 + b^2)
θ = arctan (b/a) = inverse of tan (b/a) , where b is im(z) and a is re(z)
Example:
z = 4 + 3i
r = √(4^2 + 3^2) = 5
θ = arctan(3/4) = 36.9°
polar form: 5cis36.9° = 5(cos36.9° + isin36.9°)
Real-Life Applications
Complex numbers are very useful, especially to engineers.
Signal Processing
It is useful in technologies, especially wireless and cellular technologies. It can also be used to monitor brain waves.
Electricity
Alternating current (AC) electricity switches between a sine wave’s negative and positive. When combining AC currents, the waves may not match properly, making it very difficult. By using imaginary current and real numbers, it allows those who works with AC electricity to perform calculations and prevent being electrocuted.
source: https://www.livescience.com/42748-imaginary-numbers.html
IB Learner Profile
Thinkers – having to think creatively and critically when working with numbers that don’t even exist (imaginary numbers)
Communicators – expressing concepts to others, teaching and telling them about something you learn about

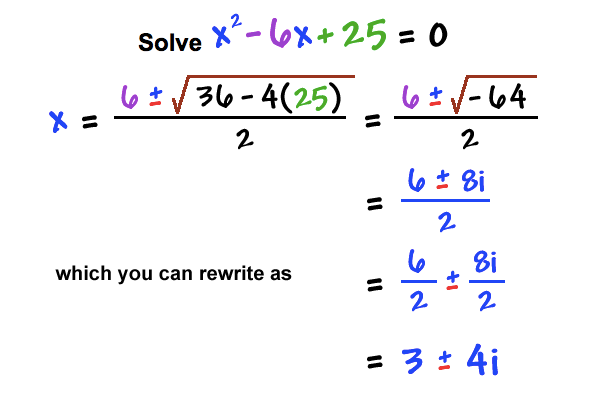

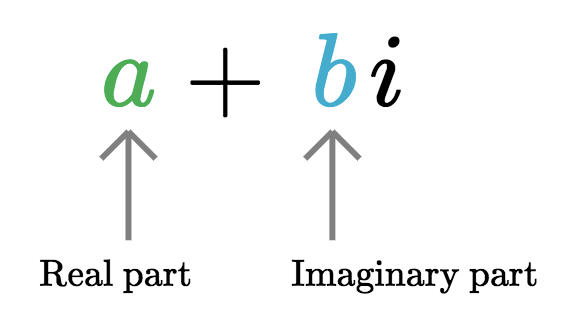
Wow, this really is a well explained blog about complex and imaginary numbers. I always thought when you root a -1, it wouldnt give out any value or number. But now i know it gives out an inaginary number! I was shocked to see that imaginary numbers (i) can be represented in the calculator after pressing MODE then CMPLX. You explained the argand diagram straightforward and it allows the readers to understand the concept with ease, including me. Its also astonishing to me how imaginary and complex numbers can be used for electricity and signals. In my opinion, it could be better if you explained the real life applications abit with more detail. But other than that, its a really amazing blog as you explained such a bewildering topic with ease and simplicity. Great work!
LikeLike
As mentioned above, I have seen the symbol ‘i’ in my calculator when solving quadratic equations and I always wondered what it really meant. Taking a read of this blog about imaginary numbers, I finally realized that it involved the square rooting which is in the formula to find the roots of a quadratic equation. It was also new to me that you could use a CMPLX mode on a calculator which will enable you to root a negative number, because usually as you have also said it will just show up as an error. It was really easy to understand complex numbers with the real and imaginary parts which can also be plotted on an Argand diagram — which, speaking of it, I thought that the image of the Argand diagram was really useful. Although the modulus-argument form came to me as an alien language when I was looking through it at first, I came across the example which was greatly helpful to me as it was much easier to comprehend. The real-life applications as well were interesting and good to know as I wouldn’t have guessed that non-existent numbers would be be put to use in such important fields which build our modern world today. Lastly, the comical images were a nice addition to the blog as it lifted up the mood a little. Overall, I think you have successfully portrayed the two IB learner profiles which you mentioned with this well-written blog. It was great to read about a fairly difficult topic which I would have otherwise found dull!
LikeLike
This blog explains a lot in detail of imaginary and complex numbers which I have often heard of but just never understood about them. I always thought that you will not get a number when you have to square root a negative number since when I input it in the calculator it will only say math error which makes me think that it does not exist until now. After reading this blog it shows me that in replacement of negative square roots which does not exist, it is replaced with imaginary numbers. I was actually surprised to see how easy it is to find out about this in the calculator, you just need to convert your calculator to complex mode and thats it. That is how simple it is but somehow I could never figure it out until I have read this blog. I am also surprised to the fact that you could apply imaginary numbers to electricity and signals. Overall I think that this blog was done brilliantly since you have found a way to project your data in pictures and comics which makes it eye catching towards the readers and making them easier to understand.
LikeLike
This blog is very informative and simple to understand. I love how you write the definition of each mathematical term and continue your post with examples and applications. It makes it easier for the readers to understand your concepts. After reading this blog I now know the difference between real and imaginary numbers, I know what “i” stands for in maths terminology and how to plot complex numbers in the cartesian plane and how to write it in modulus-argument form. Your blog post is simple to understand, and it can be used for a source of study.
LikeLike